
![]() whether they are synergic or net positive (increasing order), neutral or no change
whether they are synergic or net positive (increasing order), neutral or no change
![]() (static order), or adversary or net negative (decreasing order). Here the defined
(static order), or adversary or net negative (decreasing order). Here the defined
![]() directions of the X and Y axes, take on significance.
directions of the X and Y axes, take on significance.
![]() or net positive (inreasing order), it is longer than
or net positive (inreasing order), it is longer than
![]() the radius of the zero-zero circle.
the radius of the zero-zero circle.
![]() (+, +) quadrant. A net
(+, +) quadrant. A net
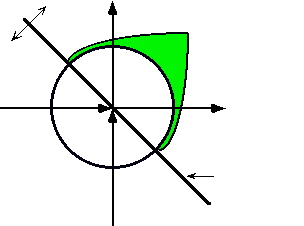
![]() synergic co-Action vector
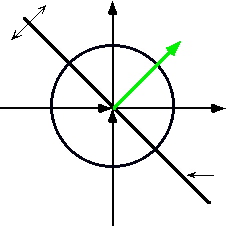
synergic co-Action vector![]() is shown in the diagram below in green ink.
is shown in the diagram below in green ink.
![]() Y
Y
(-,+)![]() (0, +)syntropy
(0, +)syntropy
![]() as a result of the relationship. The arrowhead is in the (+, +) quadrant so both are
as a result of the relationship. The arrowhead is in the (+, +) quadrant so both are
![]() winning. Their order
winning. Their order![]() in increasing. The position is equally distant from both the X
in increasing. The position is equally distant from both the X
![]() and Y
and Y![]() axis so they are winning equally.
axis so they are winning equally.
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() when they began the relationship. They have both won. They have both gained. And,
when they began the relationship. They have both won. They have both gained. And,
![]() they have benefited equally from the relationship. The individual order
they have benefited equally from the relationship. The individual order![]() of both X and
of both X and
![]() Y has increased because of their interaction.
Y has increased because of their interaction.
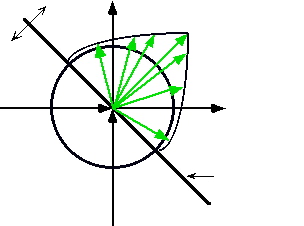
![]() shifting the reference perimeter away from the origin. The perimeter of the reference
shifting the reference perimeter away from the origin. The perimeter of the reference
![]() zero-zero circle
zero-zero circle![]() can only shift in the defined directions of the X and Y axes. Thus all
can only shift in the defined directions of the X and Y axes. Thus all
![]() net positive co-Actions will lie outside the zero-zero circle.
net positive co-Actions will lie outside the zero-zero circle.
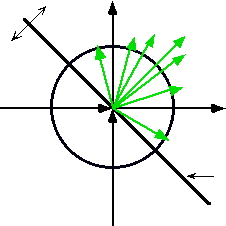
![]() synergic co-Actions. The sum of their
synergic co-Actions. The sum of their
![]() order together
order together![]() is greater than the sum of their order
is greater than the sum of their order![]() individually.
individually.
![]() sometimes X wins more than Y
sometimes X wins more than Y
![]() and sometimes X loses. We also see that sometimes Y wins more than X and sometimes
and sometimes X loses. We also see that sometimes Y wins more than X and sometimes
![]() Y loses.
Y loses.
![]() Y
Y
(-,+)![]() (0, +)syntropy
(0, +)syntropy
![]() reference zero-zero circle.
reference zero-zero circle.
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() Y
Y
(-,+)![]() (0, +)syntropy
(0, +)syntropy
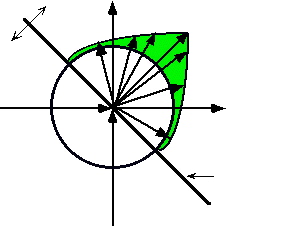
![]() — the cooperator's surplus ( +Z
— the cooperator's surplus ( +Z![]() ) outside the
) outside the
![]() zero-zero circle to the right and above the Axis of Atropy.
zero-zero circle to the right and above the Axis of Atropy.
![]() (0, +)syntropy
(0, +)syntropy
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() Y
Y
(-,+)![]() (0, +)syntropy
(0, +)syntropy
![]() green ink. This is what
green ink. This is what
![]() Haskell
Haskell![]() called the
called the ![]() cooperator's surplus
cooperator's surplus![]() ( +Z
( +Z![]() ).
).
![]() represents the net increase in order
represents the net increase in order![]() found in a synergic relationship.
found in a synergic relationship.
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

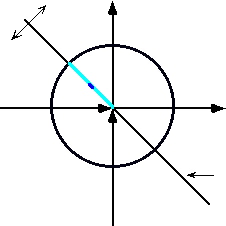
![]() or no change (static order), it is equal to the
or no change (static order), it is equal to the
![]() radius of the zero-zero circle. A net neutral
radius of the zero-zero circle. A net neutral![]() co-Action is plotted on the Axis of
co-Action is plotted on the Axis of
![]() Atropy shown below in light blue ink.
Atropy shown below in light blue ink.
![]() Y
Y
(-,+)![]() (0, +)syntropy
(0, +)syntropy
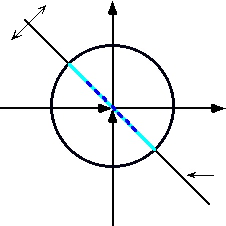
![]() is hi-lighted in dark blue
is hi-lighted in dark blue![]() to better
to better
![]() designate the reality of Y’s winning at the expense of X’s losing. The position of the
designate the reality of Y’s winning at the expense of X’s losing. The position of the
![]() dark blue dot
dark blue dot![]() shows that X's position is shifted to the right of the Y Axis and that Y's
shows that X's position is shifted to the right of the Y Axis and that Y's
![]() position is shifted above the X axis.
position is shifted above the X axis.
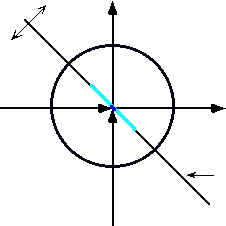
![]() in which X and Y have simply drawn
in which X and Y have simply drawn
![]() (as in win, lose
(as in win, lose![]() or draw).neither of them are winning or losing. Their relationship
or draw).neither of them are winning or losing. Their relationship
![]() has had no effect on each others condition. Their order
has had no effect on each others condition. Their order![]() has remained the same.
has remained the same.
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() Y
Y
(-,+)![]() (0, +)syntropy
(0, +)syntropy
![]() overlap, but
overlap, but
![]() we can distinguish them by their centers.
we can distinguish them by their centers.
![]() (0, +)syntropy
(0, +)syntropy
![]() sometimes X wins to Y’s loss and
sometimes X wins to Y’s loss and
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

above the Y axis represents Y’s win at the total expense of X. The net neutral co-Action
centered to the far right and below the X axis represents X’s win at the total expense
of Y. The net neutral co-Action centered at the ORIGIN (0, 0) represents X and Y both
drawing neither winning or losing. The four other net neutral co-Actions fall
somewhere in between.
![]() a net adversary co-Action. Haskell used the convention of drawing the co-Action
a net adversary co-Action. Haskell used the convention of drawing the co-Action
![]() vector from the position inside the zero-zero circle representing X and Y’s condition
vector from the position inside the zero-zero circle representing X and Y’s condition
![]() from the direction of the
from the direction of the![]() (-,-)
(-,-)![]() quadrant to the (0,0) ORIGIN.
quadrant to the (0,0) ORIGIN.
![]() is shown below in red ink.
is shown below in red ink.
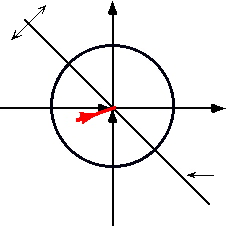
![]() (0, +)syntropy
(0, +)syntropy
![]() and terminates there. However, it is the position of the back or but end of the vector,
and terminates there. However, it is the position of the back or but end of the vector,
![]() where the guide feathers on an arrow would be found that accurately depicts X and
where the guide feathers on an arrow would be found that accurately depicts X and
![]() Y’s condition. Below I have plotted seven net adversary co-Actions.
Y’s condition. Below I have plotted seven net adversary co-Actions.
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken