
![]() (of order) and not positive
(of order) and not positive
integers. And, the zeroes represent states of no change (of order), rather than an
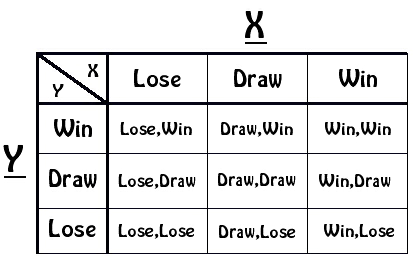
integer with no content. Or, in the language of games: Lose, Win, or Draw.
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

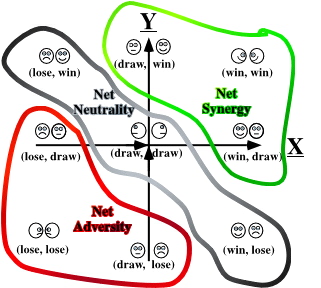
![]() Adversity, and Net Neutality are represented on Haskell's PCS.
Adversity, and Net Neutality are represented on Haskell's PCS.
![]() need a initial reference device. Recall our initial vectors:
need a initial reference device. Recall our initial vectors:

![]() Vector
Vector


![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

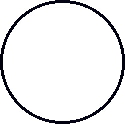
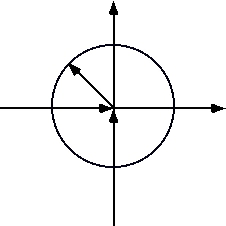
![]() area represents the initial state of the “union” X
area represents the initial state of the “union” X![]() and Y
and Y![]() as a “single” system.
as a “single” system.


Co-Action
Circle
X + Y
![]() Circle
Circle![]() as the fourth axis of the Periodic Coordinate System. This circle represents the
as the fourth axis of the Periodic Coordinate System. This circle represents the
![]() state of the union at the beginning of a relationship. It is the geometric sum of (X) and
state of the union at the beginning of a relationship. It is the geometric sum of (X) and
![]() (Y) at the initiation of their co-Action. This reference circle is made by sweeping a
(Y) at the initiation of their co-Action. This reference circle is made by sweeping a
![]() neutral Co-Action vector, ro, around the ORIGIN.
neutral Co-Action vector, ro, around the ORIGIN.
![]() or co-Action
or co-Action![]() has a synergic
has a synergic![]() or
or
![]() net (+) positive
net (+) positive![]() effect (increase in order), an adversary
effect (increase in order), an adversary![]() or net (-) negative
or net (-) negative![]() effect
effect
![]() (decrease in order), or a neutral (0)
(decrease in order), or a neutral (0)![]() or no effect at all (no change in order) . You
or no effect at all (no change in order) . You
![]() must have a reference, what was the state of the system before before the co-Action
must have a reference, what was the state of the system before before the co-Action![]() is
is
![]() initiated — the condition of the individuals before their relationship
initiated — the condition of the individuals before their relationship![]() begins. This is
begins. This is
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() (0, 0) circle.
(0, 0) circle.
![]() Perhaps an even better name might be the Circle of Neutrality. This circle represents
Perhaps an even better name might be the Circle of Neutrality. This circle represents
![]() a net neutral
a net neutral![]() relationship between (X) & (Y). But, regardless what we call it, the area
relationship between (X) & (Y). But, regardless what we call it, the area
![]() of this zero-zero circle
of this zero-zero circle![]() represents the geometric sum of X
represents the geometric sum of X![]() and Y’s condition at the
and Y’s condition at the
![]() start of the relationship. This represents the simple sum of their individual order
start of the relationship. This represents the simple sum of their individual order
![]() before their interaction.
before their interaction.
![]() at any point, the magnitudes of (X) and (Y) are equal but their signs are opposite so the
at any point, the magnitudes of (X) and (Y) are equal but their signs are opposite so the
![]() net co-Action is zero. He called this the Axis of Atropy.
net co-Action is zero. He called this the Axis of Atropy.
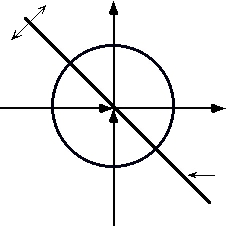
![]() (0, +)syntropy
(0, +)syntropy
![]() than the radius of the zero-zero circle are net
than the radius of the zero-zero circle are net
![]() synergic (increasing order). Those co-Action vectors that are equal
synergic (increasing order). Those co-Action vectors that are equal![]() to the radius of
to the radius of
![]() the zero-zero circle are net neutral (static order). And, those co-Action vectors that
the zero-zero circle are net neutral (static order). And, those co-Action vectors that
![]() are
are![]() less
less![]() than the radius of the zero-zero circle are net adversary (decreasing order).
than the radius of the zero-zero circle are net adversary (decreasing order).
![]() and entropic
and entropic![]() process are separated by the "Axis of Atropy".
process are separated by the "Axis of Atropy".
![]() That which is to the right and up from the axis of atropy is net synergic. That which
That which is to the right and up from the axis of atropy is net synergic. That which
![]() is left and below the axis of atropy is net adversary. And that which falls on the axis
is left and below the axis of atropy is net adversary. And that which falls on the axis
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

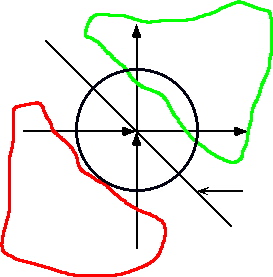
![]() Net
Net
Synergy
![]() Net
Net
Adversity
![]() Net
Net
Neutrality
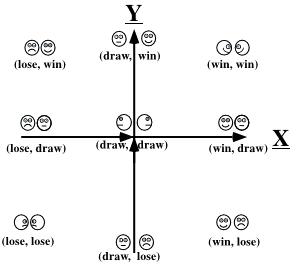
![]() ready to use the PCS to examine some relationships. Again recall our initial vectors:
ready to use the PCS to examine some relationships. Again recall our initial vectors:

![]() Vector
Vector
![]() arrow tip is used when the direction of the vector also has special meaning. In the
arrow tip is used when the direction of the vector also has special meaning. In the
![]() Periodic Coordinate System
Periodic Coordinate System![]() vectors are used to represent order
vectors are used to represent order![]() which has both
which has both
![]() quantity and quality. The condition of an individual has both quantity and
quantity and quality. The condition of an individual has both quantity and
![]() quality.The direction of the vectors will be discussed later. For now, we can then sum
quality.The direction of the vectors will be discussed later. For now, we can then sum
![]() our vectors and examine the net effect without concern for direction.
our vectors and examine the net effect without concern for direction.
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() positive (increasing order).
positive (increasing order).


![]() Neutral
Neutral
![]() order).
order).

![]() Adversary
Adversary
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken




![]() (
( ![]() X
X![]() +
+ ![]() Y
Y![]() )
)
Net Positive
![]() Synergic
Synergic



No Change
Neutral


![]() (X
(X![]() + Y
+ Y![]() )
)
Net Negative
![]() Adversary
Adversary

![]() co-Action
co-Action
![]() vectors. That is what is the effect of the relationship on the conditions of (X) and (Y).
vectors. That is what is the effect of the relationship on the conditions of (X) and (Y).
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken