
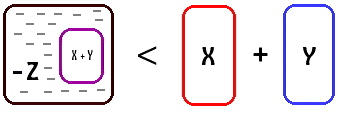
![]() striking differences. In the adversary class, there is a net loss (loss of order). The
striking differences. In the adversary class, there is a net loss (loss of order). The
![]() 'parts' lose something, They are less together than they would be apart. Haskell called
'parts' lose something, They are less together than they would be apart. Haskell called
![]() the adversary loss
the adversary loss![]() (the loss of order)
(the loss of order)![]() in the adversary relationship
in the adversary relationship![]() "the
"the
![]() conflictor's deficit". The neutral class reveals no change. They are the same
conflictor's deficit". The neutral class reveals no change. They are the same
![]() together as they would be apart (the order within is the same). However, in the
together as they would be apart (the order within is the same). However, in the
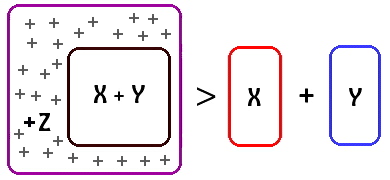
![]() synergic class, there is a net gain(gain of order). The 'parts' gain something, they
synergic class, there is a net gain(gain of order). The 'parts' gain something, they
![]() are more together than they would be apart. Haskell called the synergic gain
are more together than they would be apart. Haskell called the synergic gain![]() (the
(the
![]() gain of order)
gain of order)![]() in the synergic relationship the "cooperator's surplus".
in the synergic relationship the "cooperator's surplus".
![]() and the
and the
![]() cooperator’s surplus. We can represent the adversary loss
cooperator’s surplus. We can represent the adversary loss![]() as
as![]() ( - Z ), and the
( - Z ), and the
![]() synergic gain
synergic gain![]() as
as![]() ( + Z ).This would alter our diagrams as follows:
( + Z ).This would alter our diagrams as follows:
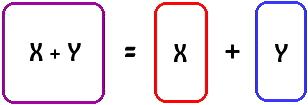
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() benefited by the relationship. The relationship is either neutral, adversary, or
benefited by the relationship. The relationship is either neutral, adversary, or
![]() synergic. The effect can also be partial. There may be relationships that are partially
synergic. The effect can also be partial. There may be relationships that are partially
![]() neutral, and/or partially adversary, and/or partially synergic.
neutral, and/or partially adversary, and/or partially synergic.
For humans, each participant determines for himself whether a relationship is
![]() synergic or adversary. This is determined from his point of view, and he cannot be
synergic or adversary. This is determined from his point of view, and he cannot be
![]() fooled. He is either more happy, more effective, more productive because of the
fooled. He is either more happy, more effective, more productive because of the
![]() relationship; or he is less happy, less effective, less productive because of the
relationship; or he is less happy, less effective, less productive because of the
![]() relationship, or he is unchanged by the relationship. The truth is in the eye of the
relationship, or he is unchanged by the relationship. The truth is in the eye of the
![]() beholder.The effect can be partial. There may be relationships that are partially
beholder.The effect can be partial. There may be relationships that are partially
![]() synergic, and/or partially neutral, and/or partially adversary.
synergic, and/or partially neutral, and/or partially adversary.
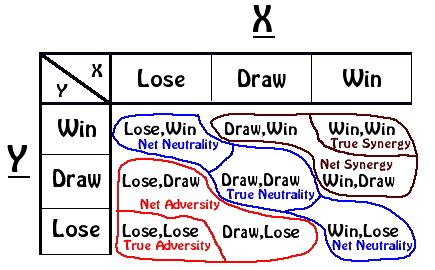
True synergy exists only when all 'parts' are benefited by the relationship True
![]() synergy is WIN-WIN. True synergy is +,+. True synergy maximizes the synergic
synergy is WIN-WIN. True synergy is +,+. True synergy maximizes the synergic
![]() gain
gain![]() — maximizes (
— maximizes (![]() Z
Z![]() ).
).
![]() exists when all participants are more happy, more
exists when all participants are more happy, more
![]() effective, and more productive. True synergy maximizes
effective, and more productive. True synergy maximizes![]() the cooperator’s
the cooperator’s
![]() surplus.
surplus.
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() much farther.
much farther.
![]() Periodic Coordinate System
Periodic Coordinate System
![]() Coordinate System. This system first appeared in 1940 as the Coaction Compass. It is
Coordinate System. This system first appeared in 1940 as the Coaction Compass. It is
![]() a geometric tool used to help visualize and graph the resultants of adversary, neutral,
a geometric tool used to help visualize and graph the resultants of adversary, neutral,
![]() and synergic relationships. Harold Cassidy
and synergic relationships. Harold Cassidy![]() explains:
explains:
![]() Periodic classification of the chemical elements. Mendeleev recognized a key
Periodic classification of the chemical elements. Mendeleev recognized a key
![]() variable to categorizing the atomic elements was their atomic weight. Today,
variable to categorizing the atomic elements was their atomic weight. Today,
![]() later scientists standing on Medeleev’s shoulders have replaced atomic
later scientists standing on Medeleev’s shoulders have replaced atomic
![]() weight
weight![]() by the more operationally constant property atomic number.
by the more operationally constant property atomic number.
![]() Periodicity is displayed by the properties of the chemical elements when the
Periodicity is displayed by the properties of the chemical elements when the
![]() elements are arranged according to increasing atomic number. Haskell found
elements are arranged according to increasing atomic number. Haskell found
![]() evidence that not only the Kingdom of Atoms, but that of Nuclei, of Plants, of
evidence that not only the Kingdom of Atoms, but that of Nuclei, of Plants, of
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

variables are properly chosen. This choice depends on cybernetic analysis, and
its application leads directly to a sub pattern know as “Co-Action” ”11
![]() powerful tool for analyzing relationships. As example, I will analyze the relationship
powerful tool for analyzing relationships. As example, I will analyze the relationship
![]() between two humans, but Haskell used the Periodic Coordinate System (PCS) to
between two humans, but Haskell used the Periodic Coordinate System (PCS) to
![]() analyze relationships within all seven “kingdoms” — particles, atoms, molecules, geoid
analyze relationships within all seven “kingdoms” — particles, atoms, molecules, geoid
![]() systems, plants, animals, and humans. It can just as easily applied to groups of
systems, plants, animals, and humans. It can just as easily applied to groups of
![]() animals or humans, communities or nations.
animals or humans, communities or nations.
![]() provides a symbolic representation of the nine
provides a symbolic representation of the nine
![]() possibilities whenever ‘parts’ relate with other ‘parts’ to form ‘wholes’ or unities, and
possibilities whenever ‘parts’ relate with other ‘parts’ to form ‘wholes’ or unities, and
![]() whenever choices are made by the ‘parts’ within the ‘whole’ or unity. This of course
whenever choices are made by the ‘parts’ within the ‘whole’ or unity. This of course
![]() applies equally well to Young’s
applies equally well to Young’s![]() Stages ofProcess
Stages ofProcess![]() in Universe — Light, Particles,
in Universe — Light, Particles,
![]() Atoms, Molecules, Plants, Animals, and Humans.
Atoms, Molecules, Plants, Animals, and Humans.
![]() scientifically as a single system. From the perspectic of synergic science, you and
scientifically as a single system. From the perspectic of synergic science, you and
![]() the individual you are in relationship with form a “unity” — a “whole”. This is
the individual you are in relationship with form a “unity” — a “whole”. This is
![]() regardless of your awareness or intention.
regardless of your awareness or intention.
![]() represent your condition both quanitatively and qualitatively at the beginning of
represent your condition both quanitatively and qualitatively at the beginning of
![]() the relationship. Geometrically, we can represent your condition by a vector.
the relationship. Geometrically, we can represent your condition by a vector.
![]() quanitatively and qualitatively by the vector Y.
quanitatively and qualitatively by the vector Y.
![]() Harold Cassidy, Introduction to FULL CIRCLE: The Moral Force of Unified Science, Gordon and
Harold Cassidy, Introduction to FULL CIRCLE: The Moral Force of Unified Science, Gordon and
![]() Breach, New York, 1972
Breach, New York, 1972
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

![]() and Y, will usually differ. In
and Y, will usually differ. In
![]() this example,the X
this example,the X![]() vector is longer meaning that X’s condition is greater than Y’s at
vector is longer meaning that X’s condition is greater than Y’s at
![]() the beginning of the relationship, but this is arbitrary to this example.Now when X
the beginning of the relationship, but this is arbitrary to this example.Now when X
![]() and Y
and Y![]() relate, we represent their “union” as a “single” system. We geometrically sum
relate, we represent their “union” as a “single” system. We geometrically sum
![]() their vectors. This produces a co-Action vector that then represents the unity of their
their vectors. This produces a co-Action vector that then represents the unity of their
![]() relationship.
relationship.

![]() Vector
Vector
![]() Periodic Coordinate System’s X
Periodic Coordinate System’s X![]() and Y
and Y![]() axis.
axis.
Periodic Coordinate
System
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

Cartesian Coordinate
System
![]() negative integers, the X-axis
negative integers, the X-axis![]() is left to right, and the
is left to right, and the![]() Y-axis
Y-axis![]() from below to above.
from below to above.

Periodic Coordinate
System
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken

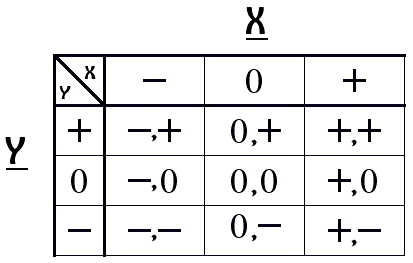
![]() and Y
and Y![]() axis of the Periodic Coordinate System.
axis of the Periodic Coordinate System.

![]() to be mindful that the minus signs represent loss
to be mindful that the minus signs represent loss![]() (of order)
(of order)![]() and not
and not
![]() Chapter 5
Chapter 5
![]() TrustMark 2002 by Timothy Wilken
TrustMark 2002 by Timothy Wilken